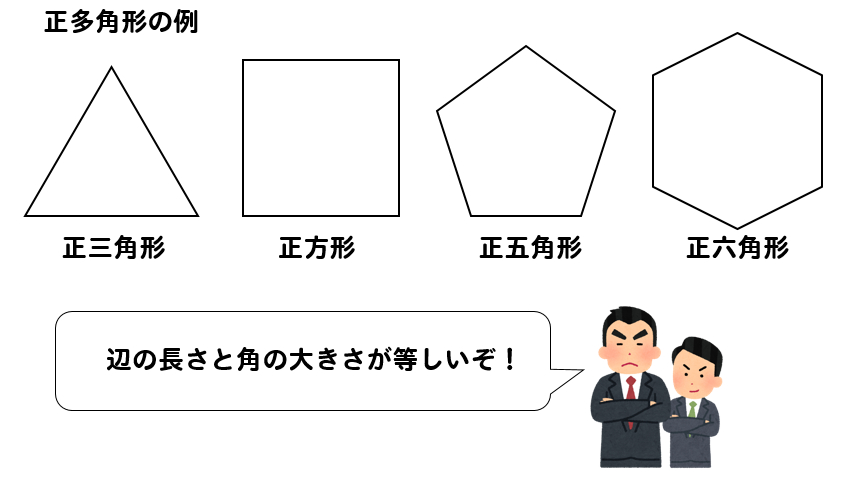
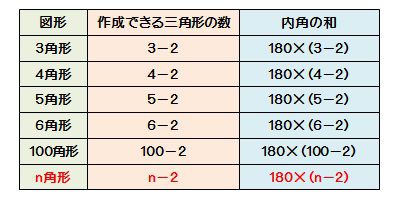
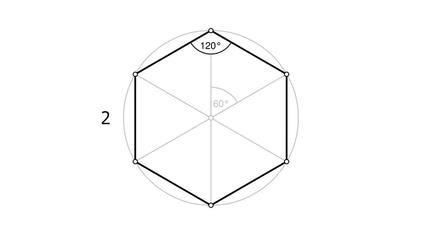
分子は多角形の内角の和を出す計算ね。 上に載せた記事で 説明はしてある。 そしてそれを3で割る。 もちろんこの3は三角形だから。 そうすれば60度と答えが出る。 ok？ で、今回の問題は160度っていってるでしょ？ じゃあこの写真みたいに 計算してみよう。正多角形とは、すべての辺、角の大きさが等しい多角形のことをいいます。 つまり、 正多角形の1つ分の内角は、内角の和を等分することで求めれます。 例 (正三角形) 内角の和180° ⇒ 1つ分の内角\(180\div3=\color{red}{60°}\) （正六角形）③ 多角形の内角の和を求める方法を導き出 す。 ↓ 7 図・表・式・グラフに表現したり， よみとる ④ nに具体的な値を代入し，いろいろな多 角形の内角の和を求める ↓ 1 類推する ⑤ 多角形の内角の和を求める方法を異なる 方法で導き出す。 準備するもの
多角形 内角 -多角形 内角の求め方" /> 上8 角形角度 Hd壁紙画像fhd
多角形 内角の求め方
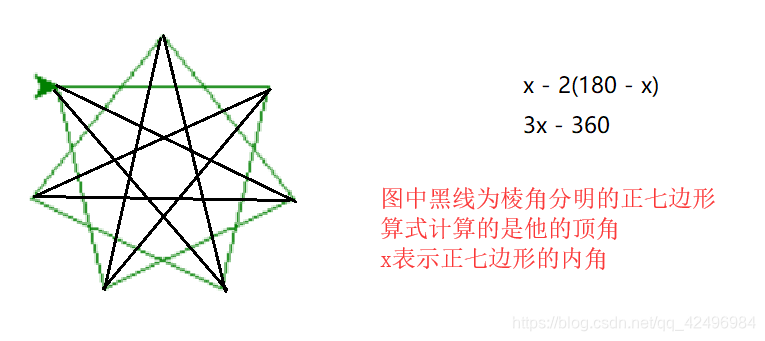
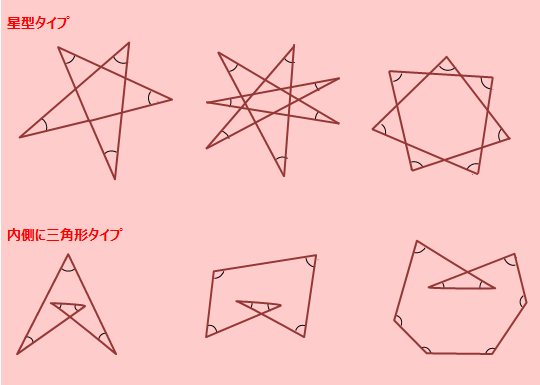
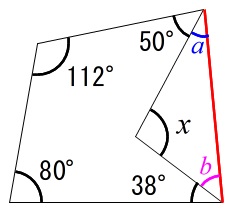
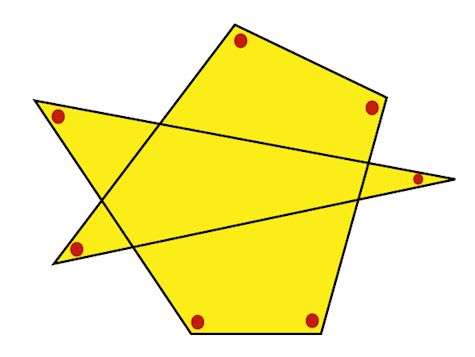
多角形 内角の求め方-こんにちは、ウチダショウマです。 今日は、中学2年生で習う 「多角形・正多角形の角度」 について、まずは多角形の内角の和・外角の和を考察し、次に正多角形の一つの内角・外角の求め方を考察します。 証明や練習問題なども扱っていますので、ぜひご覧ください♪ 多角形の内角の和2－4－1 星型多角形の内角の和 教材（問題場面） 図のように5つの点A，B，C，D， Eがある。点Aから左回りに1つとば しで点を順に結んでいくと星形五角形 ができる。その内角（∠a～∠e）の和 をいろいろな方法で求めてみよう。 H
多角形 内角 -多角形 内角の求め方"> 
正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
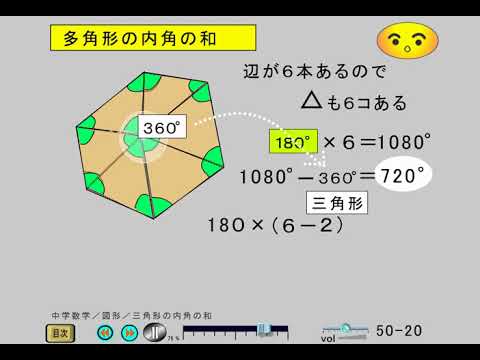
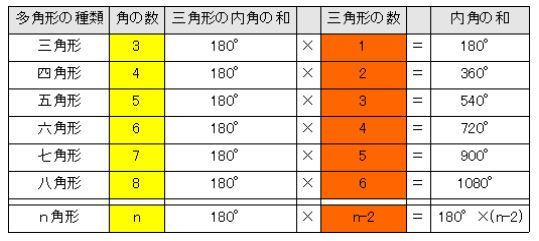
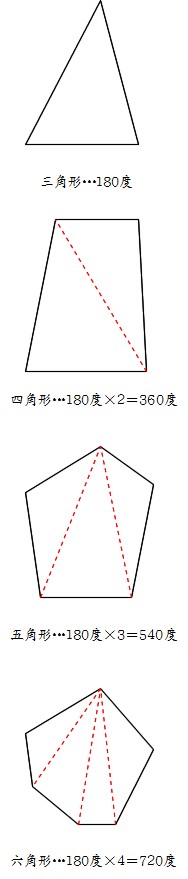
内角の和 三角形の内角の和は \(180°\) 四角形の内角の和は \(360°\) これは小学校で学習しましたし、暗記もできていることと思います。 では、 五角形の内角の和は何度でしょうか。 六角形の内角の和は何度でしょうか。 七角形の内角の和は何度でしょうか。まず、多角形の内角の和を計算する簡単な公式がこれです。 n角形の内角の和 = 180 × (n – 2) この、 多角形の内角の和についてなるべくシンプル簡単に紹介していきます。 基本的な図形の内角の和は皆さん知っていると思います。 （三角形の内角の和） = 180°分子は多角形の内角の和を出す計算ね。 上に載せた記事で 説明はしてある。 そしてそれを3で割る。 もちろんこの3は三角形だから。 そうすれば60度と答えが出る。 ok？ で、今回の問題は160度っていってるでしょ？ じゃあこの写真みたいに 計算してみよう。
内角の和 三角形の内角の和は \(180°\) 四角形の内角の和は \(360°\) これは小学校で学習しましたし、暗記もできていることと思います。 では、 五角形の内角の和は何度でしょうか。 六角形の内角の和は何度でしょうか。 七角形の内角の和は何度でしょうか。③ 多角形の内角の和を求める方法を導き出 す。 ↓ 7 図・表・式・グラフに表現したり， よみとる ④ nに具体的な値を代入し，いろいろな多 角形の内角の和を求める ↓ 1 類推する ⑤ 多角形の内角の和を求める方法を異なる 方法で導き出す。 準備するもの凹多角形の内角の和が180°×(n2)であることを証明でちゃんと書きたい者です。 質問1 「凹多角形の内角の和」と「凹多角形の外角の和」の証明は、どちらを先にやるべきでしょうか？ 片方が出ればもう片方は容
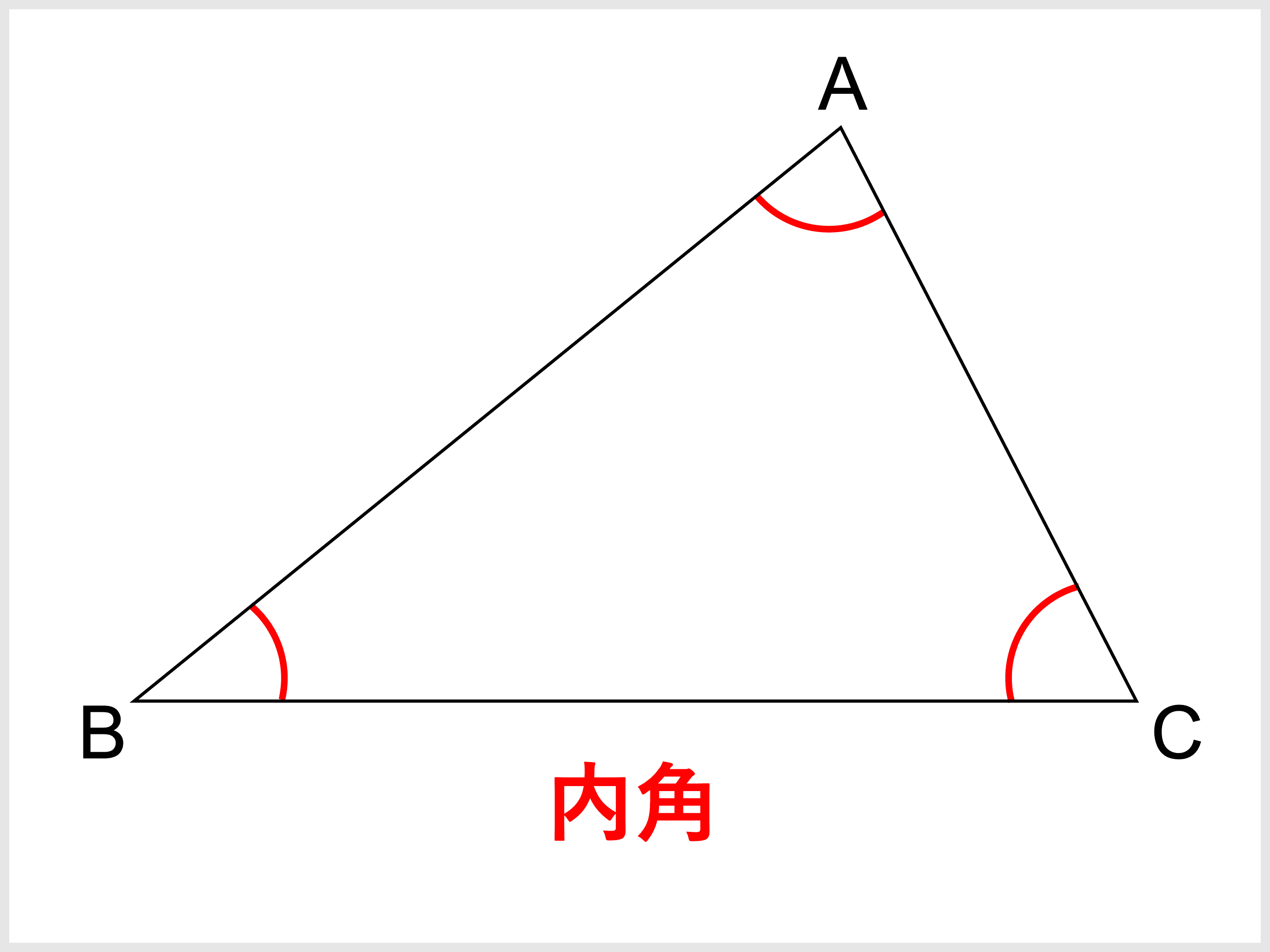
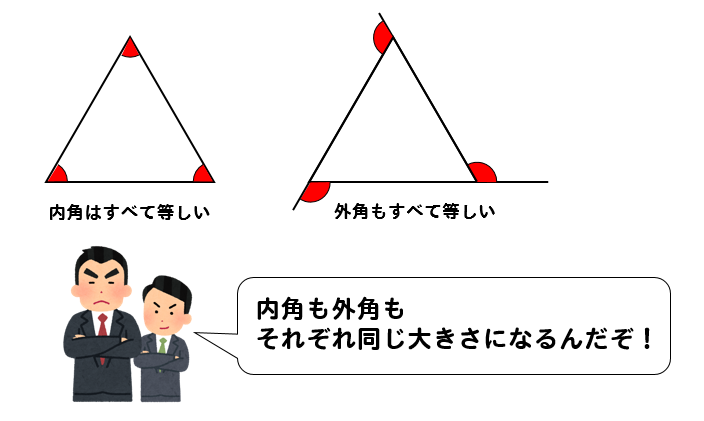
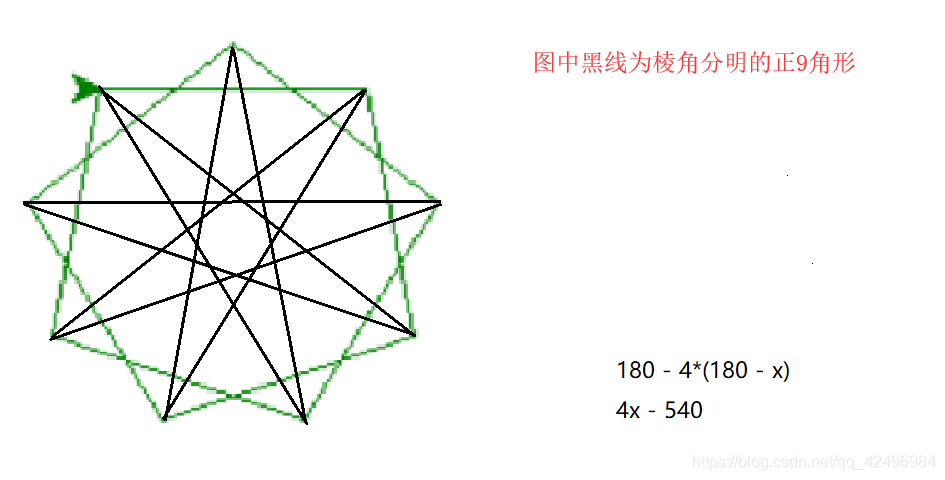
こんにちは、ウチダショウマです。 今日は、中学2年生で習う 「多角形・正多角形の角度」 について、まずは多角形の内角の和・外角の和を考察し、次に正多角形の一つの内角・外角の求め方を考察します。 証明や練習問題なども扱っていますので、ぜひご覧ください♪ 多角形の内角の和多角形の内角の和の求め方はご存知ですか？ 180×(n2)です。 そして今回の図形をn角形とし、内角の和は140n。これを方程式にします。 180×(n2)=140n 180n360=140n 40n=360 n=9 よって九角形となります。三角形の内角と外角 $ ABC$ において，$\angle A，\angle B，\angle C$ を，$ ABC$ の内角といいます． また，下図の $\angle ACD$ や $\angle BCE$ のように，一つの辺とその隣の辺の延長がつくる角を，外角といいます． さて，三角形の内角と外角について，次の重要な事実が成り立ちます．
多角形 内角 -多角形 内角の求め方"> 多角形の内角と外角 思考力を鍛える数学
多角形 内角 -多角形 内角の求め方"> 正多角形の1つの内角 外角を求める方法を問題解説 数スタ
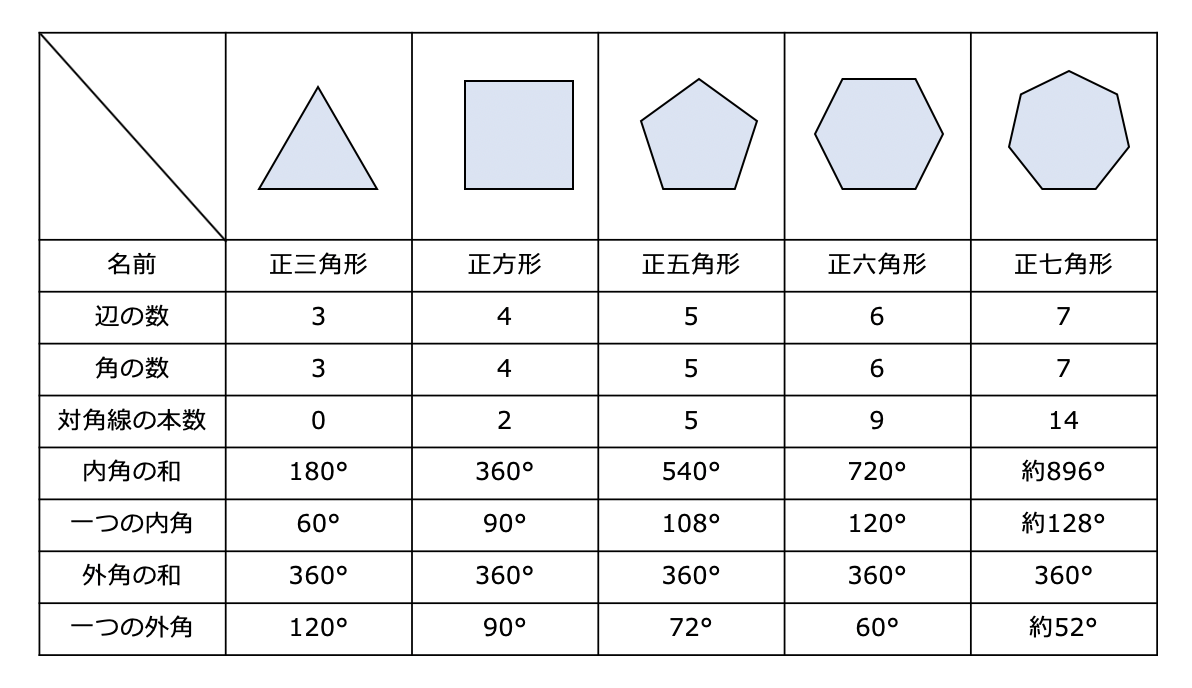
正多角形とは、 「すべての辺の長さが等しく、すべての内角の大きさが等しい多角形」 を指します。 よって、多角形の内角の和の公式より、正多角形の一つ一つの内角は 180°×(n −2) n 180 ° × (n − 2) n と求めることができます。まず、多角形の内角の和を計算する簡単な公式がこれです。 n角形の内角の和 = 180 × (n – 2) この、 多角形の内角の和についてなるべくシンプル簡単に紹介していきます。 基本的な図形の内角の和は皆さん知っていると思います。 （三角形の内角の和） = 180°内角の和が180度になる理由など下記が参考になります。 内角の和と三角形の関係は？1分でわかる和の値、証明、外角との関係 外角と内角の違い 外角と内角の違いを下記に示します。 外角 ⇒ 多角形の外側にできる角 内角 ⇒ 多角形の内側にできる角
多角形 内角 -多角形 内角の求め方"> 中2数学 多角形の内角 外角 図形の合同 ひっそりと物理や数学を解説する
多角形 内角 -多角形 内角の求め方"> 多角形の内角や外角の和 中学数学に関する質問 勉強質問サイト
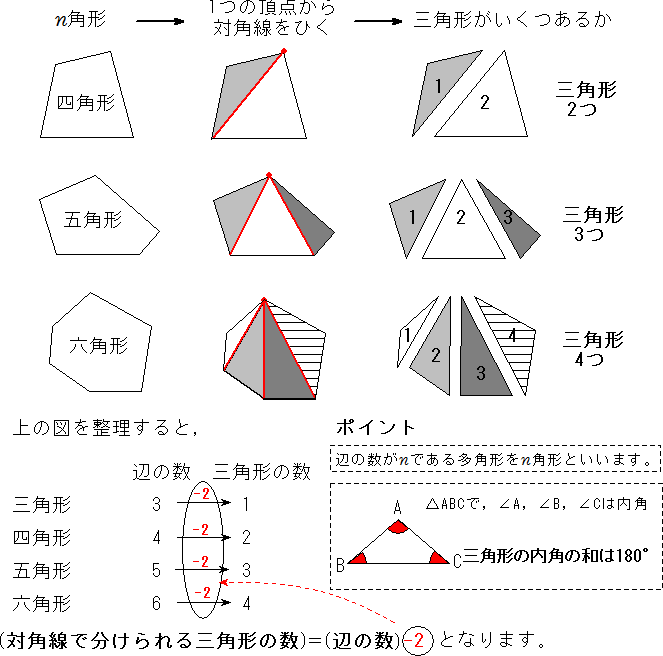
正多角形とは、すべての辺、角の大きさが等しい多角形のことをいいます。 つまり、 正多角形の1つ分の内角は、内角の和を等分することで求めれます。 例 (正三角形) 内角の和180° ⇒ 1つ分の内角\(180\div3=\color{red}{60°}\) （正六角形）多角形の内角の和はどのようにして求めるのかを説明していきます。 ポイントは「 三角形に分ける 」ということです。 前回 三角形の内角の和は\(180^\circ\) であることを確認しています。多角形の内角の和については、以下のように増えていきます。 三角形：内角の和は180° 四角形：内角の和は360° 五角形：内角の和は540° 六角形：内角の和は7° このように、 多角形では辺が一つ増えるごとに内角の和は180増加します。
多角形 内角 -多角形 内角の求め方"> 内角和 内角和公式 五边形内角和 N边形内角和公式
多角形 内角 -多角形 内角の求め方"> 中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su
正多角形の1つの内角の大きさを出したいときは、 内角の和を頂点の数でわればいいんだ。 内角の和「180°×（n2）」を、 頂点の数「n」でわると正多角形の1つの内角の大きさになるよ。 180× (n2)/n どの内角も同じ大きさだからね！多角形の内角の和の公式 三角形の内角の和： 180° 180 ° 四角形の内角の和： 360° 360 ° 五角形の内角の和： 540° 540 °株式会社ベネッセコーポレーションのプログラミング教育の取り組みや、プログラミング教育に関する国内外のニュースや事例を紹介するWebページです。 小5算数 内角の大きさを求めて正多角形を作図しよう について紹介します。
多角形 内角 -多角形 内角の求め方"> 50 グレア多角形内角 壁紙おしゃれトイレ
多角形 内角 -多角形 内角の求め方"> 八角形内角 N边形内角和公式 正边形内角公式 多边形外角公式
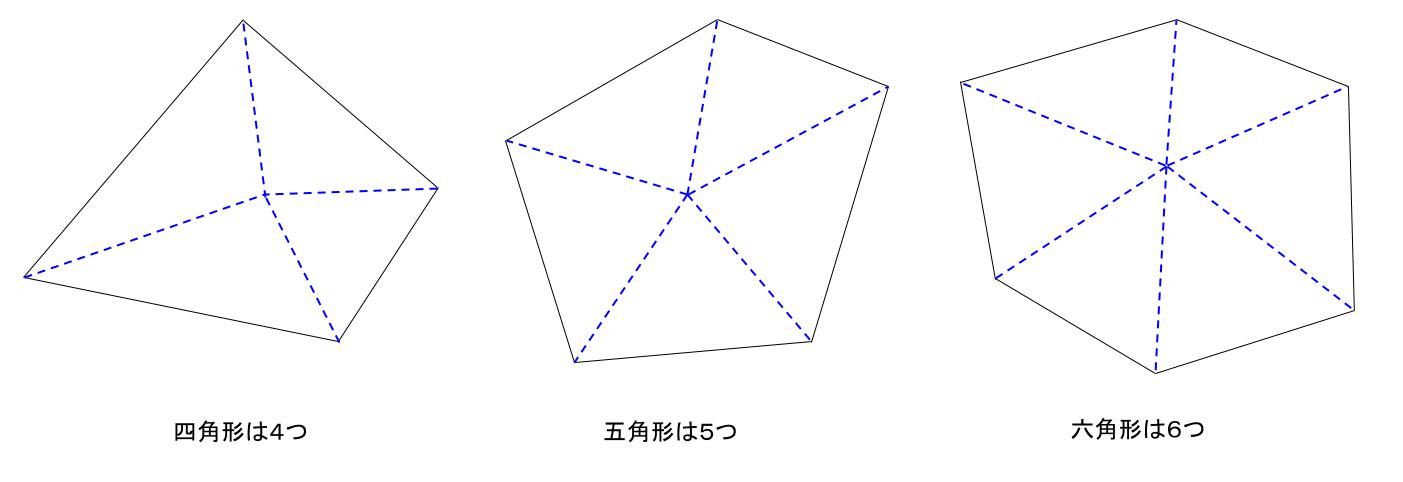
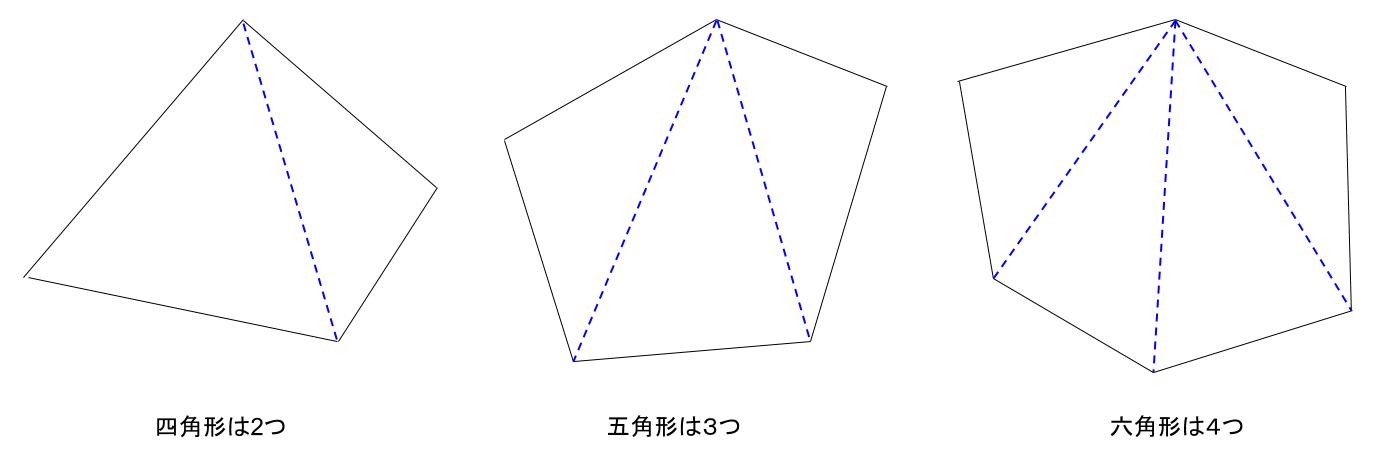
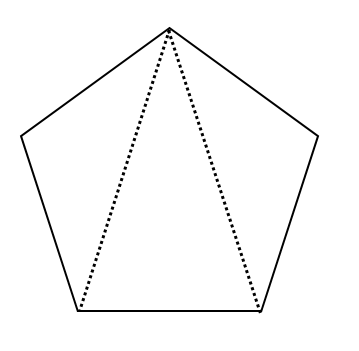
多角形の内角の和はどのようにして求めるのかを説明していきます。 ポイントは「 三角形に分ける 」ということです。 前回 三角形の内角の和は\(180^\circ\) であることを確認しています。
多角形 内角 -多角形 内角の求め方"> 多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
多角形 内角 -多角形 内角の求め方"> 新しい六角形内角 壁紙配布
多角形 内角 -多角形 内角の求め方"> 八角形内角 N边形内角和公式 正边形内角公式 多边形外角公式
多角形 内角 -多角形 内角の求め方"> 内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学
多角形 内角 -多角形 内角の求め方"> 多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
多角形 内角 -多角形 内角の求め方"> 50 グレア多角形内角 壁紙おしゃれトイレ
多角形 内角 -多角形 内角の求め方"> 内角和公式 五边形内角和 多边形的外角和 N边形的内角和是
多角形 内角 -多角形 内角の求め方"> 五边形内角是多少 三人行教育网 Www 3rxing Org
多角形 内角 -多角形 内角の求め方"> 如何计算内角总和 建议 February 21
多角形 内角 -多角形 内角の求め方"> 中学数学 図形と証明 50 10 30 多角形の内角の和 Youtube
多角形 内角 -多角形 内角の求め方"> Junior High数学的数学 多角形の内角と外角 筆記 Clear
多角形 内角 -多角形 内角の求め方"> 内角和 内角和公式 五边形内角和 N边形内角和公式
多角形 内角 -多角形 内角の求め方"> Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码
多角形 内角 -多角形 内角の求め方"> 中2数学 多角形の内角 外角 図形の合同 ひっそりと物理や数学を解説する
多角形 内角 -多角形 内角の求め方"> 内角和 内角和公式 五边形内角和 N边形内角和公式
多角形 内角 -多角形 内角の求め方"> 多边形的内角和与外角和 Ppt Ppt课件下载 人人ppt
多角形 内角 -多角形 内角の求め方"> 小学校5年 算数 正多角形の角の大きさ Youtube
多角形 内角 -多角形 内角の求め方"> 正五边形的内角和是 时习社区
多角形 内角 -多角形 内角の求め方"> 新しい六角形内角 壁紙配布
多角形 内角 -多角形 内角の求め方"> 多角形の内角の和の公式と外角の和を利用した角度の求め方
内角和与三边 腾讯视频
多角形 内角 -多角形 内角の求め方"> 八边形 维基百科 自由的百科全书
多角形 内角 -多角形 内角の求め方"> 内角和 内角和公式 五边形内角和 N边形内角和公式
多角形 内角 -多角形 内角の求め方"> １つの内角が 度である正多角形の求め方 勉強好き塾長がテストで役に立つこと書いちゃうブログ 仮
多角形 内角 -多角形 内角の求め方"> 内角和公式 五边形内角和 多边形的外角和 N边形的内角和是
多角形 内角 -多角形 内角の求め方"> 中2数学 複雑な多角形 角の和 応用問題
多角形 内角 -多角形 内角の求め方"> 上8 角形角度 Hd壁紙画像fhd
多角形 内角 -多角形 内角の求め方"> 多角形の内角の和の公式を３通りの方法で証明する 具体例で学ぶ数学
多角形 内角 -多角形 内角の求め方"> 多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
多角形 内角 -多角形 内角の求め方"> 50 グレア多角形内角 壁紙おしゃれトイレ
多角形 内角 -多角形 内角の求め方"> 内角和公式和外角和公式 多边形外角公式 多边形的内角和 多边形外角
多角形 内角 -多角形 内角の求め方"> 多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
多角形 内角 -多角形 内角の求め方"> 课件 教员分享 Z1版 七年级数学 沪教版 八年级下 22 1 探索多边形的内角和 免费数学课件下载 优思教辅
多角形 内角 -多角形 内角の求め方"> 50 グレア多角形内角 壁紙おしゃれトイレ
多角形 内角 -多角形 内角の求め方"> 三角形と四角形 多角形の内角の和 中学数学 定期テスト対策サイト
多角形 内角 -多角形 内角の求め方"> 多角形の内角と外角 の問題のわからないを5分で解決 映像授業のtry It トライイット
多角形 内角 -多角形 内角の求め方"> 50 グレア多角形内角 壁紙おしゃれトイレ
多角形 内角 -多角形 内角の求め方"> １つの内角が150度の正多角形は何角形ですか 途中式も知りたいです Clear
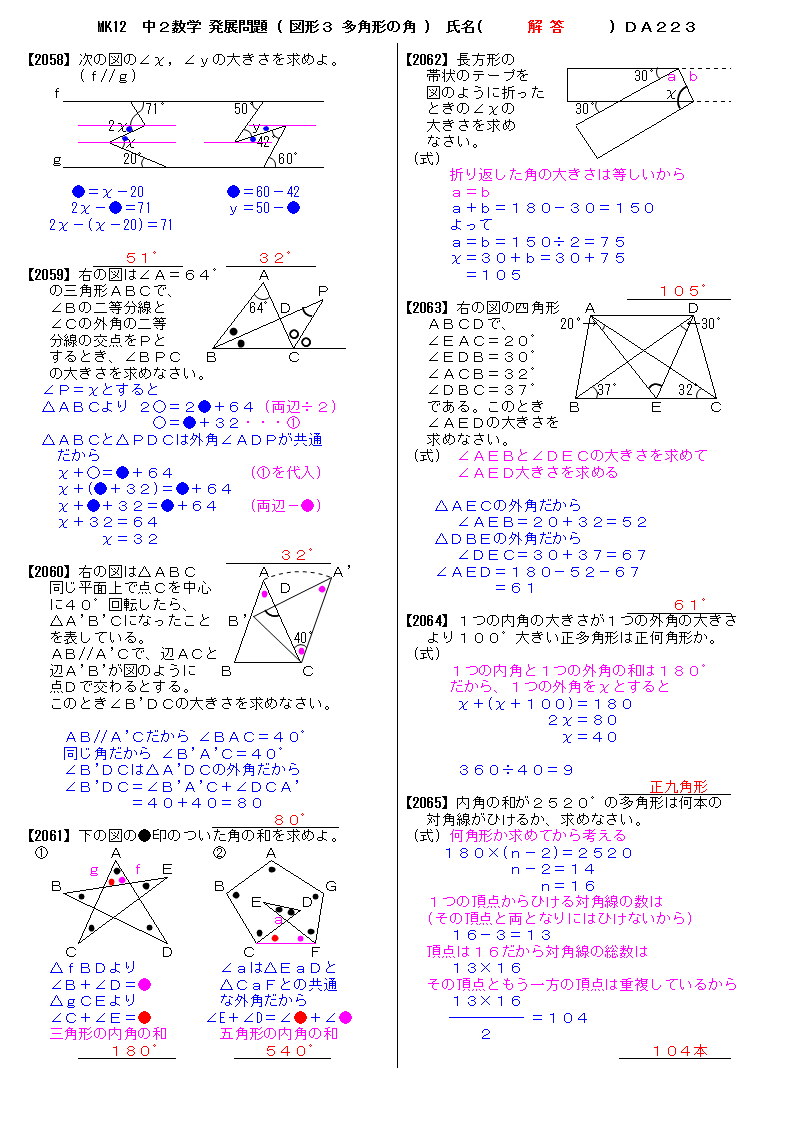
多角形 内角 -多角形 内角の求め方"> 無料 中２数学 発展問題 解答プリント 223 図形３ 多角形の角
多角形 内角 -多角形 内角の求め方"> 外角公式 内角和公式和外角和公式 正多边形外角和公式 正n边形的内角和公式
多角形 内角 -多角形 内角の求め方"> ラブリー多角形角度 久方区
多角形 内角 -多角形 内角の求め方"> 理論 特別な多角形の内角の和 Youtube
多角形 内角 -多角形 内角の求め方"> 多边形的内角
多角形 内角 -多角形 内角の求め方"> 多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
多角形 内角 -多角形 内角の求め方"> 多角形の内角と外角 アセント学習塾 塾長の こうかい 日誌
多角形 内角 -多角形 内角の求め方"> 多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
多角形 内角 -多角形 内角の求め方"> 多角形の内角と外角 の問題のわからないを5分で解決 映像授業のtry It トライイット
多角形 内角 -多角形 内角の求め方"> 内角の和の公式 内角の和が１８００ の多角形は何角形 中学や高校の数学の計算問題
多角形 内角 -多角形 内角の求め方"> 正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
多角形 内角 -多角形 内角の求め方"> Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码
多角形 内角 -多角形 内角の求め方"> 内角和 内角和公式 五边形内角和 N边形内角和公式
多角形 内角 -多角形 内角の求め方"> Junior High数学的多角形の内角と外角筆記 Clear
多角形 内角 -多角形 内角の求め方"> 多边形的内角
多角形 内角 -多角形 内角の求め方"> 六角形内角切割视频 西瓜视频
多角形 内角 -多角形 内角の求め方"> 多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
多角形 内角 -多角形 内角の求め方"> 五边形 维基百科 自由的百科全书
多角形 内角 -多角形 内角の求め方"> 多角形 の内角の角度 計算ドリル 問題集 数学fun
多角形 内角 -多角形 内角の求め方"> 证明 六边形内角和7 三种方法教会大家 哔哩哔哩 つロ干杯 Bilibili
多角形 内角 -多角形 内角の求め方"> 99以上多角形内角 Hd壁紙画像fhd
多角形 内角 -多角形 内角の求め方"> 一つの内角が160度である正多角形は正何角形ですか Clear
多角形 内角 -多角形 内角の求め方"> 正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より
多角形 内角 -多角形 内角の求め方"> 在知识迁移 问题类化中探索多角形内角和问题 参考网
多角形 内角 -多角形 内角の求め方"> 课件 教员分享 Z1版 七年级数学 沪教版 八年级下 22 1 探索多边形的内角和 免费数学课件下载 优思教辅
多角形 内角 -多角形 内角の求め方"> 一つの内角が160度である正多角形は正何角形ですか Clear
多角形 内角 -多角形 内角の求め方"> 数学 中2 51 多角形の内角と外角の和 基本編 Youtube
多角形 内角 -多角形 内角の求め方"> 99以上多角形内角 Hd壁紙画像fhd
多角形 内角 -多角形 内角の求め方"> 内角和 内角和公式 五边形内角和 N边形内角和公式
多角形 内角 -多角形 内角の求め方"> 正多角形の1つの内角 外角を求める方法を問題解説 数スタ
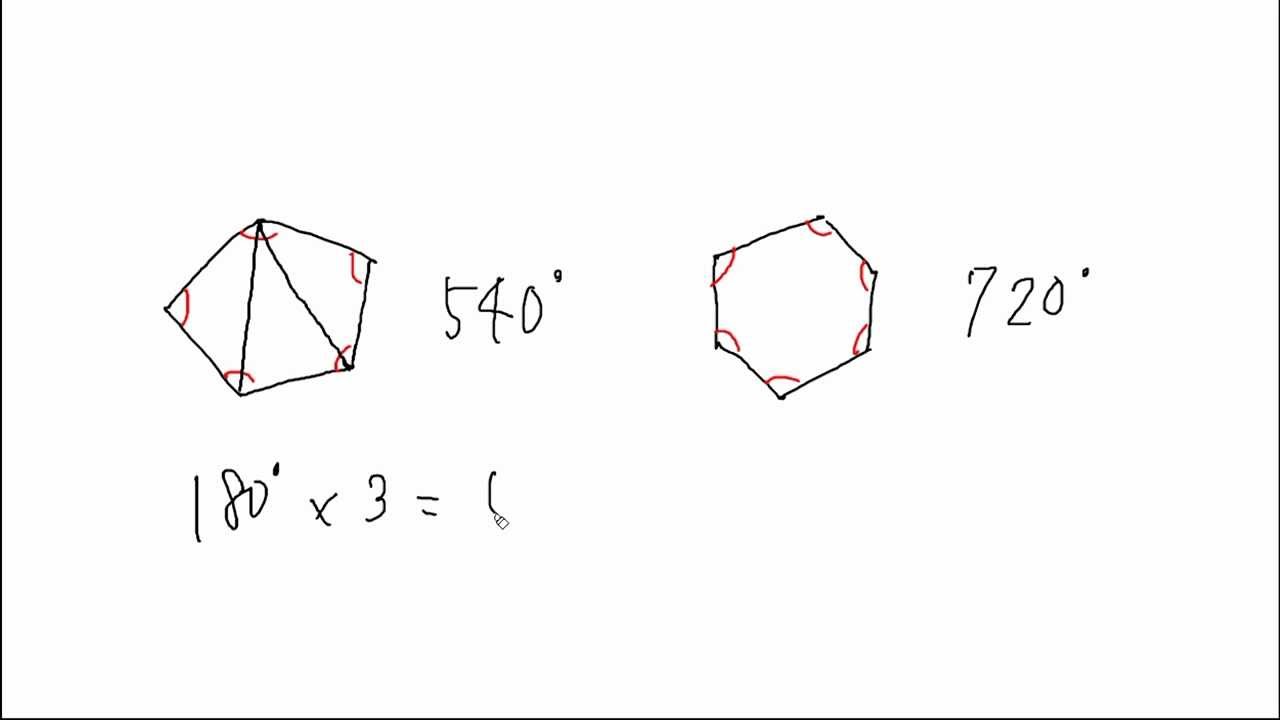多角形 内角 -多角形 内角の求め方"> 多角形の内角の和 Youtube
多角形 内角 -多角形 内角の求め方"> 内角和公式和外角和公式 多边形外角公式 多边形的内角和 多边形外角
多角形 内角 -多角形 内角の求め方"> 在知识迁移 问题类化中探索多角形内角和问题 参考网
多角形 内角 -多角形 内角の求め方"> 99以上多角形内角 Hd壁紙画像fhd
多角形 内角 -多角形 内角の求め方"> 多角形の内角の和 算数の公式覚えてますか
多角形 内角 -多角形 内角の求め方"> 50 グレア多角形内角 壁紙おしゃれトイレ
多角形 内角 -多角形 内角の求め方"> 50 グレア多角形内角 壁紙おしゃれトイレ
多角形 内角 -多角形 内角の求め方"> ラブリー多角形角度 久方区
多角形 内角 -多角形 内角の求め方"> 50 グレア多角形内角 壁紙おしゃれトイレ
多角形 内角 -多角形 内角の求め方"> 正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
多角形 内角 -多角形 内角の求め方"> 正多边形内角和公式及定义 快资讯
多角形 内角 -多角形 内角の求め方"> 99以上多角形内角 Hd壁紙画像fhd
多角形 内角 -多角形 内角の求め方"> つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト
多角形 内角 -多角形 内角の求め方"> Math 多角形の内角の和 働きアリ
正九边形求内角 腾讯视频
多角形 内角 -多角形 内角の求め方"> 正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
多角形 内角 -多角形 内角の求め方"> 内角和 内角和公式 五边形内角和 N边形内角和公式
多角形 内角 -多角形 内角の求め方"> 多角形の内角の和 は何度なのか を説明します おかわりドリル
多角形 内角 -多角形 内角の求め方"> 8边形内角和度数是什么 初三网
多角形 内角 -多角形 内角の求め方"> Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码
多角形 内角 -多角形 内角の求め方"> 内角和公式 五边形内角和 多边形的外角和 N边形的内角和是
多角形 内角 -多角形 内角の求め方"> 課題学習の指導 数学
多角形 内角 -多角形 内角の求め方"> Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码
0 件のコメント:
コメントを投稿